Cao Yi
河内塔 Hanoi Tower
问题描述。有三根杆子A,B,C。A杆上有N个(N>1)穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆:
- 每次只能移动一个圆盘;
- 大盘不能叠在小盘上面。
- 提示:可将圆盘临时置于B杆,也可将从A杆移出的圆盘重新移回A杆,但都必须尊循上述两条规则。
问:如何移?最少要移动多少次?(TODO)
这个问题源于法国数学家爱德华·卢卡斯杜撰的一个故事:傳說印度某間寺院有三根柱子,上串64个金盤。寺院裡的僧侶依照一個古老的預言,以上述規則移動這些盤子;預言說當這些盤子移動完毕,世界就會滅亡。(注:这个故事本身有点扯,因为河内在越南而不是印度。)
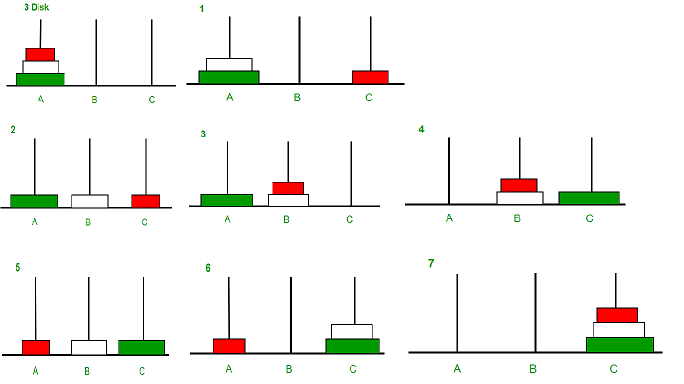
(图片来自Program for Tower of Hanoi Algorithm)
递归版本
递归方式的 Java 控制台版本:
public static void hanoi(int i, String a, String b, String c) { //以 b 为中转, 将 i 个盘子从 a 移动到 c
if (i == 1) {
move(a, c); // 直接将 a 移动到 c
} if (i > 1) {
hanoi(i-1, a, c, b); // 以 c 为中转, 将 i-1 个盘子从 a 移动到 b
move(a, c); // 直接将 a 移动到 c, 此时移动的就是最底下的那个盘子
hanoi(i-1, b, a, c); // 以 a 为中转, 将 i-1 个盘子从 b 移动到 c
}
}
public static void move(String src, String dst) {
System.out.println(src + " -> " + dst);
}
完整的代码参考这里.
Python3 可以如此写:
# hanoi tower
def hanoi(n, a, b, c): # 以 b 为中转, 将 i 个盘子从 a 移动到 c
if n == 1:
print(a, '->', c) # 直接将 a 移动到 c
return
if n > 1:
hanoi(n - 1, a, c, b) # 以 c 为中转, 将 i-1 个盘子从 a 移动到 b
print(a, '->', c) # 直接将 a 移动到 c, 此时移动的就是最底下的那个盘子
hanoi(n -1, b, a, c) # 以 a 为中转, 将 i-1 个盘子从 b 移动到 c
# sample
hanoi(3, 'A', 'B', 'C')
完整的代码参考这里.
非递归版本
TODO
河內塔是數據結構 stack 的一個經典應用。
参考:
本文从旧站搬迁而来。