Cao Yi

求平方根——牛顿迭代法

返回目录

牛顿迭代法(Newton-Raphson Method)，简单说就是先随便选个点，开始通过不断尝试，逐渐接近目标值的方法。

它并不只是适用用二次平方曲线，但数学上可以证明，用牛顿迭代法求平方根是合理的。具体证明将来再写TODO。

牛顿法求根的过程展示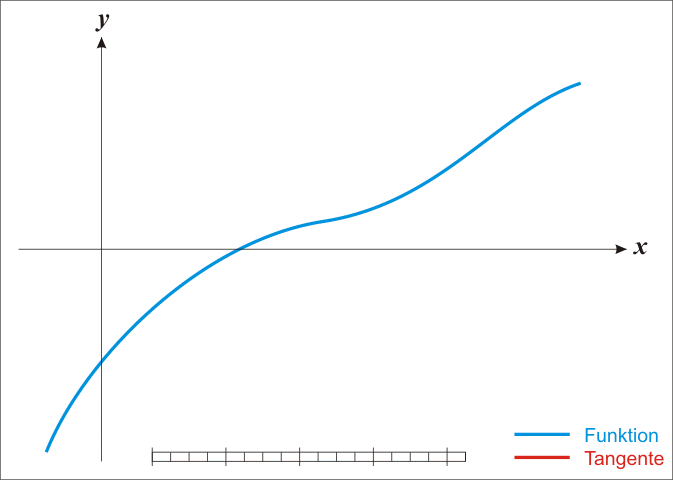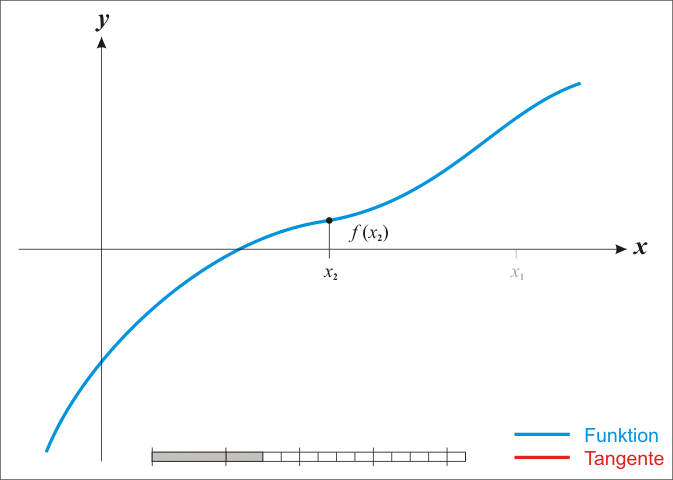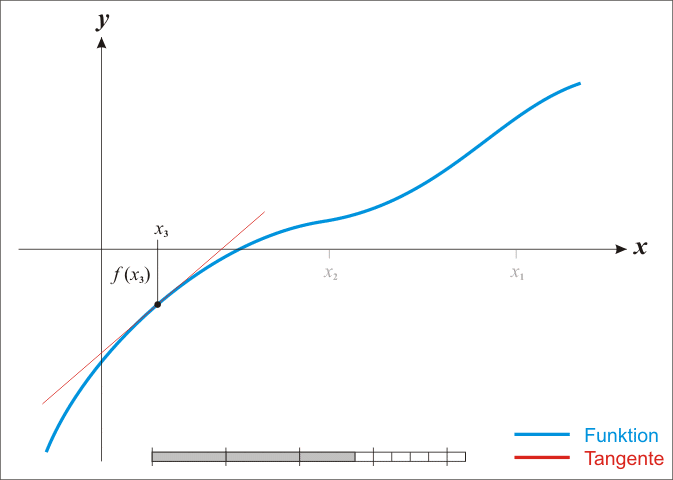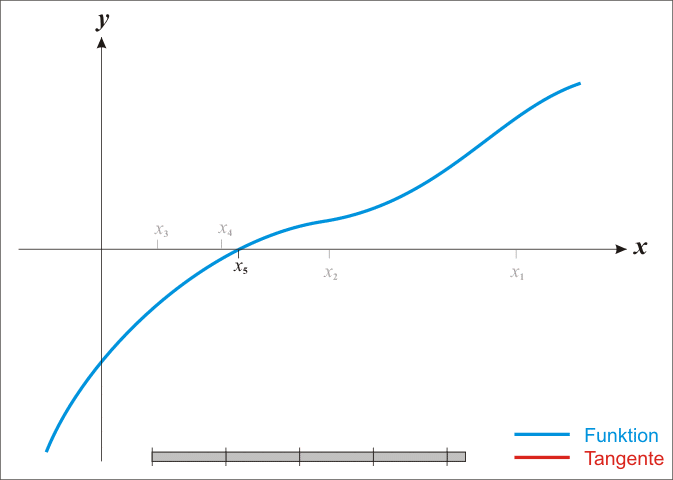： (This image is copied from https://en.wikipedia.org/wiki/File:NewtonIteration_Ani.gif)

x[n+1] = x[n] - f(x[n])/f'(x[n])

具体求解过程如下：

1. 先在函数上任选一个点
2. 作切线，和x轴相交，判断交点是否为近似解，是就跳出，否就继续下一步
3. 通过交点作x轴的垂线，和函数图像相交
4. 重复第二步，直到找出近似解

平方根求解。即求 f(x) = x^2 - N 根。

1. 先在函数上任选一个点，不妨就选N
2. 作切线，和x轴相交，判断交点是否为近似解，是就跳出，否就继续下一步
   • 斜率为 2x[n]
   • 过(x[n], f([n]))的切线是：f(x) - f(x[n]) = 2x[n] * (x - x[n]), 导入f(x) = x^2 -N 得f(x) - (x[n]^2 - N) = 2x[n] * (x - x[n])
   • 上式中 f(x) = 0时得到切线和x轴交点：x = (x[n] + N/x[n])/2
   • 将这个值代入 f(x) = x^2 - N 验算，看是否满足近似条件
3. 通过交点作x轴的垂线，和函数图像相交
4. 重复第二步，直到找出近似解

x[n+1] = x[n] - x[n]^2/（2 * x[n]) = (1/2) * x[n]

代码实现

C

double calSqrt(double number)
{
    if (number < 0)
    {
        printf("The input value should be greater than zero.");
        exit(1);
    }

    double err = 1e-15;   //设置误差范围，当误差小于这个值时认为得到准确值
    double root = number; //给平方根一个预设值，不妨从参数 n 本身开始尝试。
    while (abs(number - root * root) > err)
    {
        root = (number / root + root) / 2.0;
    }
    return root;
}

完整的代码实现参sqrt_newton.c

Java

public static double sqrt(double c) {
    if (c < 0) {
        return Double.NaN;
    }
    double err = 1e-15;
    double t = c;
    while (Math.abs(t - c / t) > err * t) {
        t = (c / t + t) / 2.0;
    }
    return t;
}

完整的代码实现参SqrtNewton.java

---

后记，因为阅读《算法·第4版》(Robert & Kevin)，书中第一章第13页（英文版在P22）提到了用牛顿迭代法求平方根，故做了一点小小的研究，记录于此。

参考：

1. 如何通俗易懂地讲解牛顿迭代法？
2. 牛顿迭代法求平方根原理, chenrenxiang
3. Newton’s method
4. C语言牛顿迭代法求平方根的过程

This site is open source. Improve this page.