Cao Yi
托勒密定理 Ptolemy’s Theorem
圆的内接四边形,对边之积的和于对角线之积相等。
如图
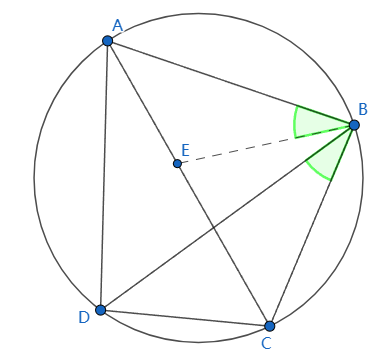
A, B, C, D四点共圆,则 $\vert AC \vert \cdot \vert BD \vert = \vert AB \vert \cdot \vert CD \vert + \vert BC \vert \cdot \vert DA \vert$
【证明】
过B点作BE于AC相交于E点,使$\angle ABE = \angle DBC$.
又 $\because \angle CDB = \angle CAB$
$\therefore \triangle BAE \sim \triangle BDC$
$\therefore \dfrac{\vert AE \vert}{\vert AB \vert} = \dfrac{\vert DC \vert}{\vert DB \vert}$
$\therefore \vert AE \vert \cdot \vert DB \vert = \vert AB \vert \cdot \vert DC \vert$
$\because \angle ABD = \angle ABE + \angle EBD = \angle DBC + \angle EBC=\angle EBC$
且 $\angle ADB = \angle ECB$
$\therefore \triangle ADB \sim \triangle ECB$
$\therefore \dfrac{\vert EC \vert}{\vert CB \vert} = \dfrac{\vert AD \vert}{\vert DB \vert}$
$\therefore \vert EC \vert \cdot \vert DB \vert = \vert CB \vert \cdot \vert AD \vert$
$\therefore \vert AE \vert \cdot \vert DB \vert + \vert EC \vert \cdot \vert DB \vert = \vert AB \vert \cdot \vert DC \vert + \vert CB \vert \cdot \vert AD \vert$
$\therefore (\vert AE \vert + \vert EC \vert ) \cdot \vert DB \vert = \vert AB \vert \cdot \vert DC \vert + \vert CB \vert \cdot \vert AD \vert$
$\therefore \vert AC \vert \cdot \vert DB \vert = \vert AB \vert \cdot \vert DC \vert + \vert CB \vert \cdot \vert AD \vert$
即 $\vert AC \vert \cdot \vert BD \vert = \vert AB \vert \cdot \vert CD \vert + \vert BC \vert \cdot \vert DA \vert$
【后记】
上周六(2023.07.22)Charles重新发现了这个定理,但没有证明出来,我尝试用余弦定理证明,但计算量非常大,放弃。本文的证明过程是从维基百科的相关词条学到的。还有其他很多证明方法,比如使用正弦定理、余弦定理、复数等工具,将来有时间再补上。