Cao Yi
Ceva 定理
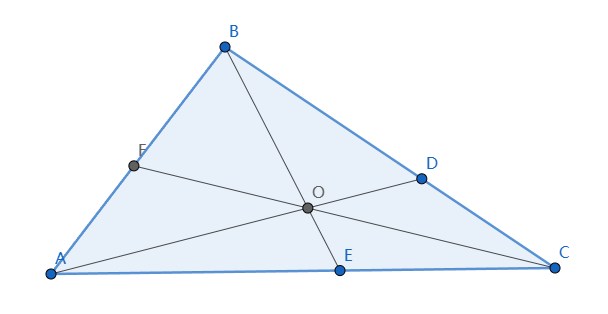
如上图,O是$\triangle ABC$中任意一点,直线AO, BO, CO分别和三角形的边相交于D, E, F, 则 $\dfrac{\vert AF \vert}{\vert FB \vert} \cdot \dfrac{\vert BD \vert}{\vert DC \vert} \cdot \dfrac{\vert CE \vert}{\vert EA \vert} = 1$
据维基百科资料,这个定理是Giovanni Ceva在1678发表的,昨天(2023.07.21)被Charles重新发现了一次。
The theorem is often attributed to Giovanni Ceva, who published it in his 1678 work De lineis rectis. But it was proven much earlier by Yusuf Al-Mu’taman ibn Hűd, an eleventh-century king of Zaragoza.
证明
根据燕尾模型,
$\dfrac{\vert AF \vert}{\vert FB \vert} = \dfrac{S_{\triangle OAC}}{S_{\triangle OBC}}$, $\dfrac{\vert BD \vert}{\vert DC \vert} = \dfrac{S_{\triangle OAB}}{S_{\triangle OAC}}$, $\dfrac{\vert CE \vert}{\vert CA \vert} = \dfrac{S_{\triangle OBC}}{S_{\triangle OAB}}$
$\therefore \dfrac{\vert AF \vert}{\vert FB \vert} \cdot \dfrac{\vert BD \vert}{\vert DC \vert} \cdot \dfrac{\vert CE \vert}{\vert EA \vert} = \dfrac{S_{\triangle OAC}}{S_{\triangle OBC}} \cdot \dfrac{S_{\triangle OAB}}{S_{\triangle OAC}} \cdot \dfrac{S_{\triangle OBC}}{S_{\triangle OAB}}= 1$
点评
这个定理看起来很整齐,结论也很简单,但发现过程却不容易。