Cao Yi
圆周角和圆心角
这是初中平面几何里的基础内容,最近Charles聊到相关的问题,记录一下。
1. 圆心角 Radius Angle
顶点在圆心,两边和圆周相交的角。
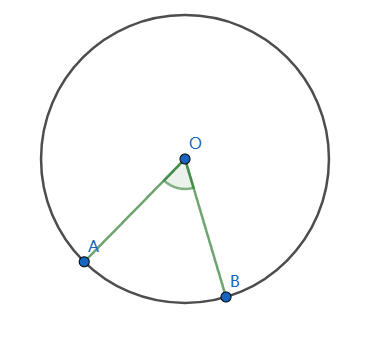
如上图, $\angle AOB$是圆O的一个圆心角,对应的弧是$\overset{\large\frown}{AB}$.
圆心角可以用对应的单位圆的弧长来表示,单位圆的圆周是$2\pi$,所以用弧长度量角的大小时,设置360$^\circ=2\pi$ rad(弧度),弧长为半径的弧对应圆心角为1.
弧长相等的弧所对的圆心角是相等的,这也是用单位圆弧长来度量角的原因。
2. 圆周角 Angle of Circumference
顶点在圆周,两边和圆周相交的角。
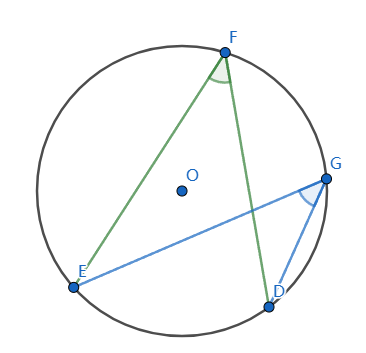
如上图$\angle EFD$和$\angle EGD$都是$\overset{\large \frown}{ED}$所对的圆周角。$\angle FEG$和$\angle FDG$也是圆周角。
一条弧有可以对应无数圆周角,它们都相等吗?且看下面的内容。
3. 圆心角和圆周角的一些性质
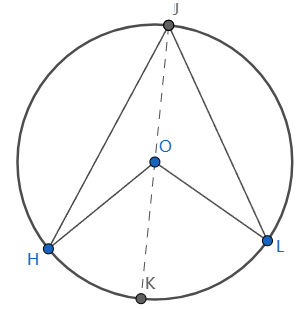
如上图,$\overset{\large \frown}{HL}$所对的圆心角和圆周角分别是$\angle HOL$和$\angle HJK$.
$\triangle HOJ$和$\triangle LOJ$是两个以半径为腰的等腰三角形
$\therefore \angle OHJ = \angle OJH$, $\angle OLJ = \angle OJL$
$\therefore \angle HOL = \angle HOK + \angle KOL = 2\angle OJH + 2\angle OJL=2(\angle OJH + \angle OJL)=2\angle HJL$
在上图中,同弧所对的圆心角是圆周角的两倍。再考察另外两种情形:
顺时针转动L,使K和L重合:
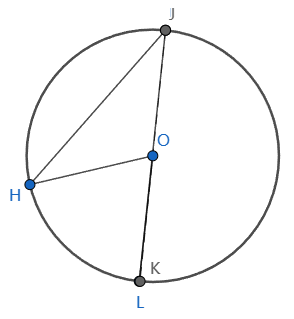
继续顺时针转动L,使K和L在JK的同一侧:
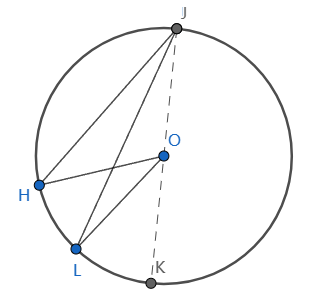
很容易看出,同弧所对的圆心角还是圆周角的两倍。
同一段弧,对应无数圆周角,和同一个圆心角,这些圆周角都等于圆心角的一半,所以同弧所对的圆周角都相等。
直径对应的圆周是半圆,对应的圆心角是$\pi$,所以直径所对的圆周角是$\dfrac{\pi}{2}$,即直径所对的圆周角是直角。