Cao Yi
Law of Cosines 余弦定理
本文中的证法二更简单好懂一些,可以直接跳过证法一先看证法二。
已知:$\triangle{ABC}$中, $\angle{A}$, $\angle{B}$, $\angle{C}$对应的三条边分别是a, b, c
求证:
- $a^2 = b^2 + c^2 -2bc\cos{\angle A}$
- $b^2 = a^2 + c^2 -2ac\cos{\angle B}$
- $c^2 = a^2 + b^2 -2ab\cos{\angle C}$
证法一
这个证明会用到了三角公式$\cos{\angle A}=\cos(\alpha + \beta)=\cos\alpha\cos\beta - \sin\alpha\sin\beta$,实际上也可以不用这个公式,只用勾股定理和诱导公式就行,参本文证法二。
分析:
设有一三角形如图所示
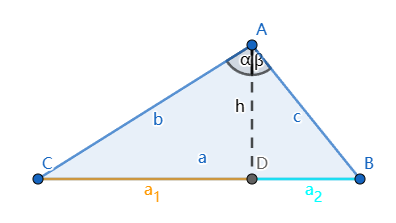
$AD \perp BC$,AD是BC上的高, 记为h.
由勾股定理可得:
$b^2=a_1^2+h^2, c^2=a_2^2+h^2$
$\therefore b^2+c^2=a_1^2+a_2^2+2h^2$
$\because a^2 = (a_1 + a_2)^2 = a_1^2+a_2^2+2a_1a_2$
$\therefore b^2+c^2-a^2=2(h^2-a_1a_2)$ 式(1)
欲证 $a^2 = b^2 + c^2 -2bc\cos{\angle A}$
即证 $b^2+c^2-a^2=2bc\cos{\angle A}$ 式(2)
如果式(1)式(2)两式右边相等即得证
即证 $bc\cos{\angle A}=h^2-a_1a_2$
即证 $\cos{\angle A}=\dfrac{h^2-a_1a_2}{bc}$ 式(3)
下面尝试计算 $\cos{\angle A}$
$\cos{\angle A}=\cos(\alpha + \beta)=\cos\alpha\cos\beta - \sin\alpha\sin\beta
=\dfrac{h}{b}\cdot\dfrac{h}{c} - \dfrac{a_1}{b}\cdot\dfrac{a_2}{c}
=\dfrac{h^2-a_1a_2}{bc}$
式(3)得证,所以 $a^2 = b^2 + c^2 -2bc\cos{\angle A}$ 成立,同理可证另外两式。
以上分析过程本身也可以作为证明过程,但也可以整理为更简单的证明形式,如下:
证明:
$\because \cos{\angle A}=…=\dfrac{h^2-a_1a_2}{bc}$
$\therefore b^2 + c^2 -2bc\cos{\angle A}
=b^2+c^2-2(h^2-a_1a_2)
=(a_1^2+h^2) + (a_2^2+h^2) - 2(h^2-a_1a_2)
=a_1^2+a_2^2+2a_1a_2
=(a_1+a_2)^2
=a^2$
当$\angle{A} \geq \dfrac{\pi}{2}$可以用上面的证明,而当$\angle{A}$为锐角时,即$\angle{A} \lt \dfrac{\pi}{2}$时,则需要下面的证明过程:
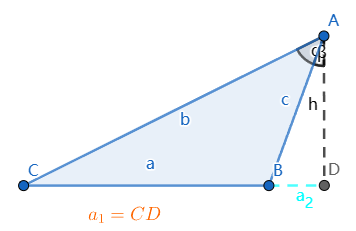
由图可知:$a=a_1-a_2$, $\angle{A}=\alpha - \beta$
$\therefore b^2 + c^2 -2bc\cos{\angle A}=b^2 + c^2 -2bc\cos{(\alpha - \beta)}
=b^2 + c^2 - 2bc(\cos\alpha\cos\beta+\sin\alpha\sin\beta)
=b^2 + c^2 - 2bc(\dfrac{h}{b}\cdot\dfrac{h}{c} + \dfrac{a_1}{b}\cdot\dfrac{a_2}{c})
=(a_1^2+h^2) + (a_2^2 + h^2) - 2bc\cdot\dfrac{h^2+a_1a_2}{bc}$
$=…
=(a_1-a_2)^2
=a^2$
综上,$a^2 = b^2 + c^2 -2bc\cos{\angle A}$得证,另外两种情况类似可证。
证法二
本证法以 $\angle B$ 为例,其余情况类似。
1. 当 $\angle{B}$ 为锐角时
继续使用前一个证法里的图,设有一三角形如图所示

$AD \perp BC$,AD是BC上的高, 记为h.
则依据勾股定理 $b^2 = h^2 + {a_1}^2$
又 $h=c\sin{\angle B}, a_1 = a - a_2 = a - c\cos{\angle B}$
$\therefore b^2 = c^2\sin^2\angle{B} + (a - c\cos{\angle B})^2$
$\therefore b^2 = c^2\sin^2\angle{B} + a^2 - 2ac\cos{\angle B}+c^2\cos^2\angle{B}$
代入 $\sin^2\angle{B} + \cos^2\angle{B} = 1$ 得:
$\therefore b^2 = a^2 + c^2 - 2ac\cos{\angle B}$
2. 当 $\angle{B}$ 为直角时
此时根据勾股定理,可得:
$b^2 = a^2 + c^2$
此时 $\cos\angle{B} = \cos(\dfrac{\pi}{2}) = 0$
$\therefore b^2 = a^2 + c^2 = a^2 + c^2 + 2ac\cos(\angle{B})$
3. 当 $\angle{B}$ 为钝角时
继续使用前一个证法里的图,设有一三角形如图所示

$AD \perp BC$,AD是BC上的高, 记为h. $D$ 在 $CB$ 的延长线上。
则依据勾股定理 $b^2 = h^2 + {(a + a_2)}^2$
又
- $h=c\sin{(\pi - \angle{B})}=c\sin\angle{B}$
- $a_2 = c\cos{(\pi - \angle{B})=-c\cos\angle{B}}$
$\therefore b^2 = c^2\sin^2\angle{B} + (a - c\cos\angle B)^2$
展开并代入 $\sin^2\angle{B} + \cos^2\angle{B} = 1$ 得:
$\therefore b^2 = a^2 + c^2 - 2ac\cos{\angle B}$
这个网站也有一个证明,它只证了相当于我这里的第一种情况,要简单一些。