Cao Yi
三角形等边对等角
等腰三角形两腰所对的角相等。
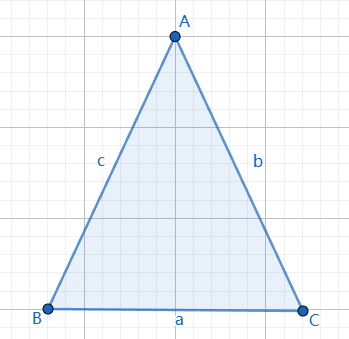
如下图,已知$\triangle ABC$的两边AB=AC,则$\angle B = \angle C$.
证明一
将$\triangle ABC$和$\triangle ACB$视为不同的三角形,利用全等三角形的性质证明$\angle B = \angle C$,详细证明过程如下。
$\because AB = AC, \angle BAC = \angle CAB, AC = AB$
根据SAS判定规则,$\triangle BAC \cong \triangle CAB$
$\therefore \angle ABC = \angle ACB$
即 $\angle B = \angle C$
证毕。
证明二
$S_{\triangle} = \dfrac{ab \sin C}{2} = \dfrac{ac \sin B}{2}$
$\therefore b \sin C = c \sin B$
$\because b = c$
$\therefore \sin C = \sin B$
$\because B \gt 0, C \gt 0 \lt B + C \lt \pi$
$\therefore B = C$
证毕。
证明三
用反证法试试。
假如 $\angle B \neq \angle C$
$\because B \gt 0, C \gt 0 \lt B + C \lt \pi$
$\therefore \sin C \neq \sin B$
$\because b = c$
$\therefore b \sin C \neq c \sin B$
$\therefore \dfrac{ab \sin C}{2} \neq \dfrac{ac \sin B}{2}$
但 $S_{\triangle} = \dfrac{ab \sin C}{2}$ 且 $S_{\triangle} = \dfrac{ac \sin B}{2}$
$\therefore S_{\triangle} \neq S_{\triangle}$ 这个结论显然错误
$\therefore$ 假设不成立
$\therefore \angle B = \angle C$