Cao Yi
三角公式 Trigonometric Formulas
1. 图像
基本三角函数在直角坐标和极坐标下的图像。
- 正弦 sine
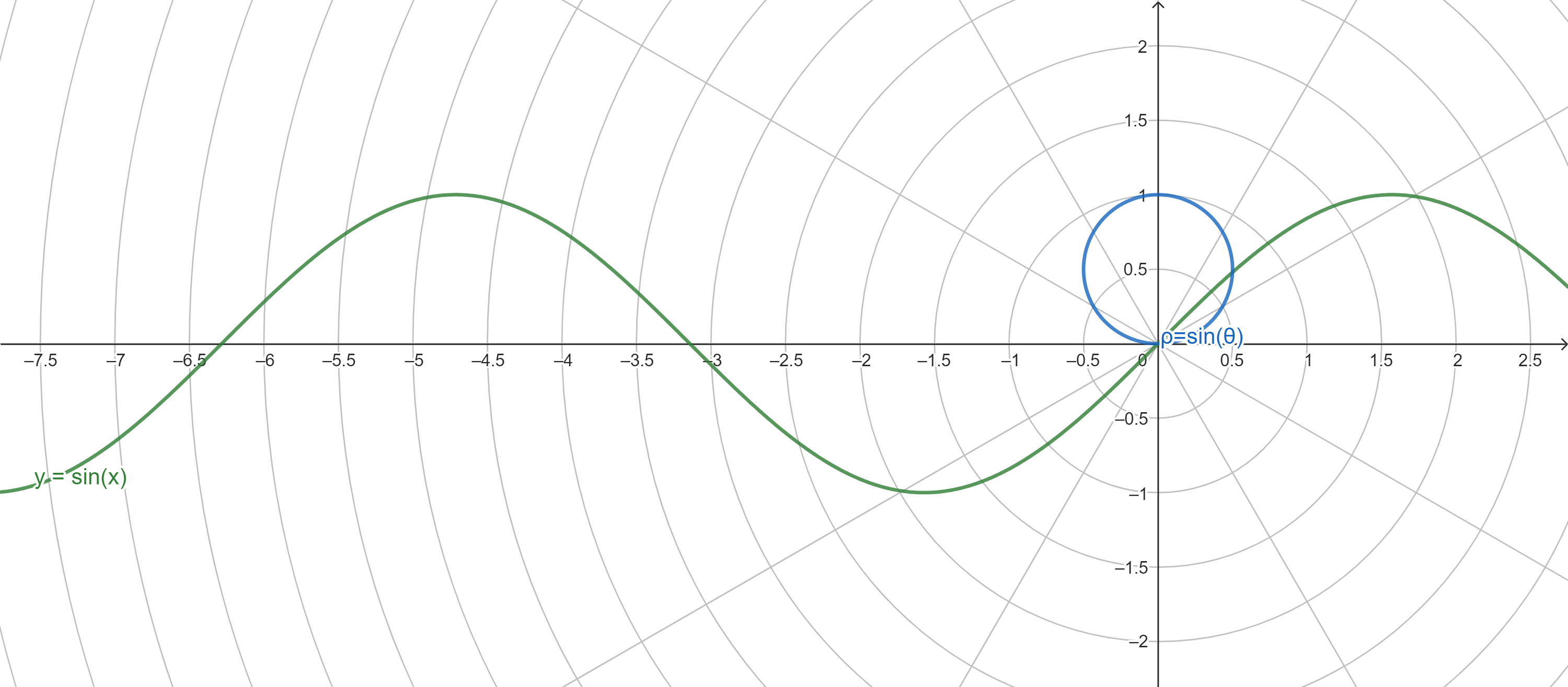
- 余弦 cosine
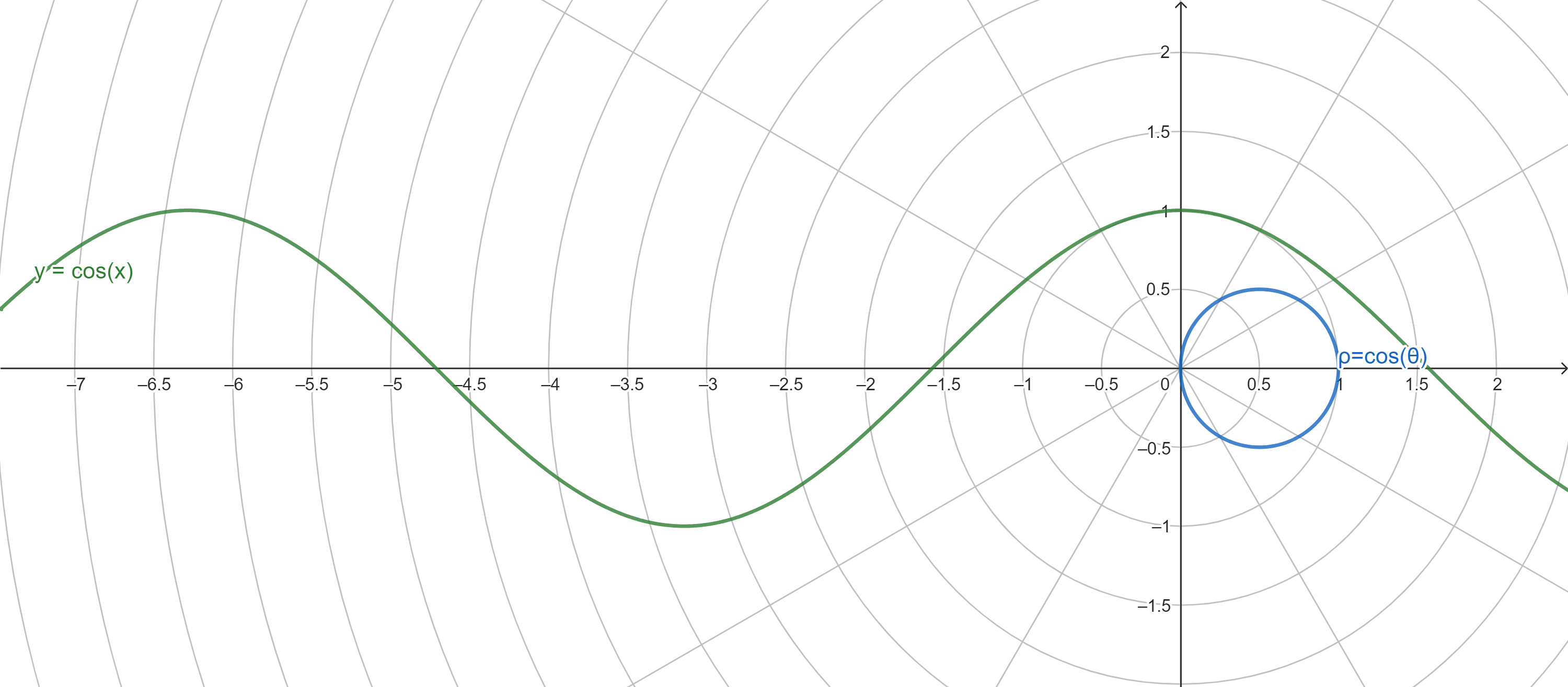
- 正切 tangent
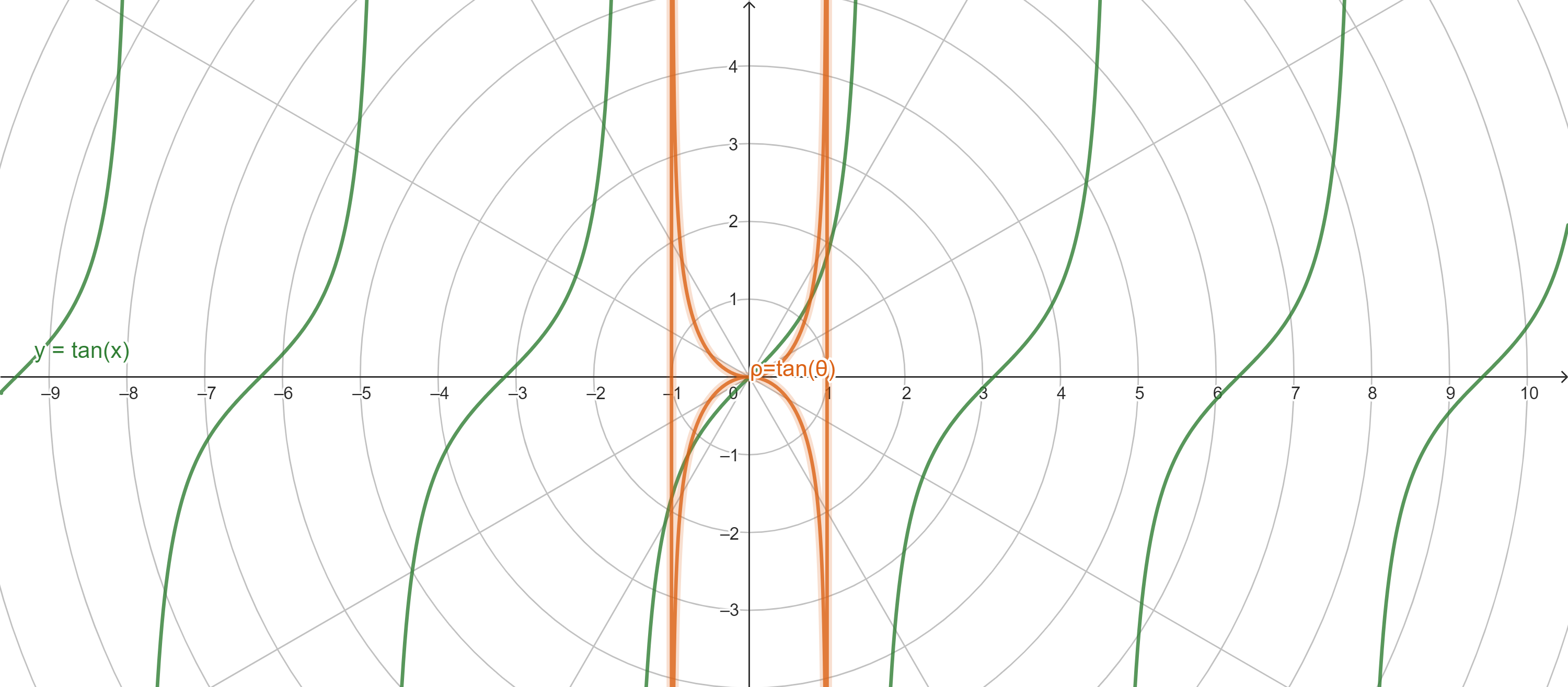
- 余切 cotangent
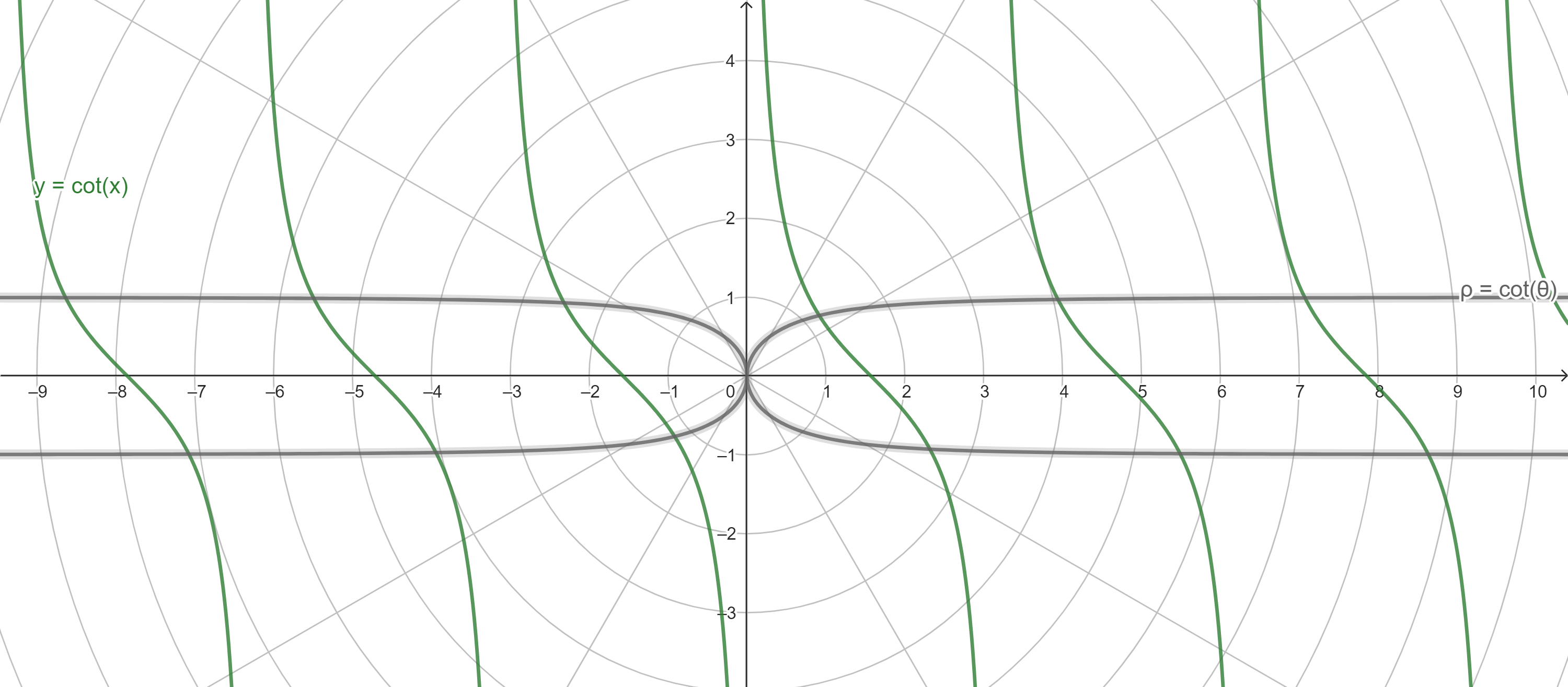
- 正割 sec
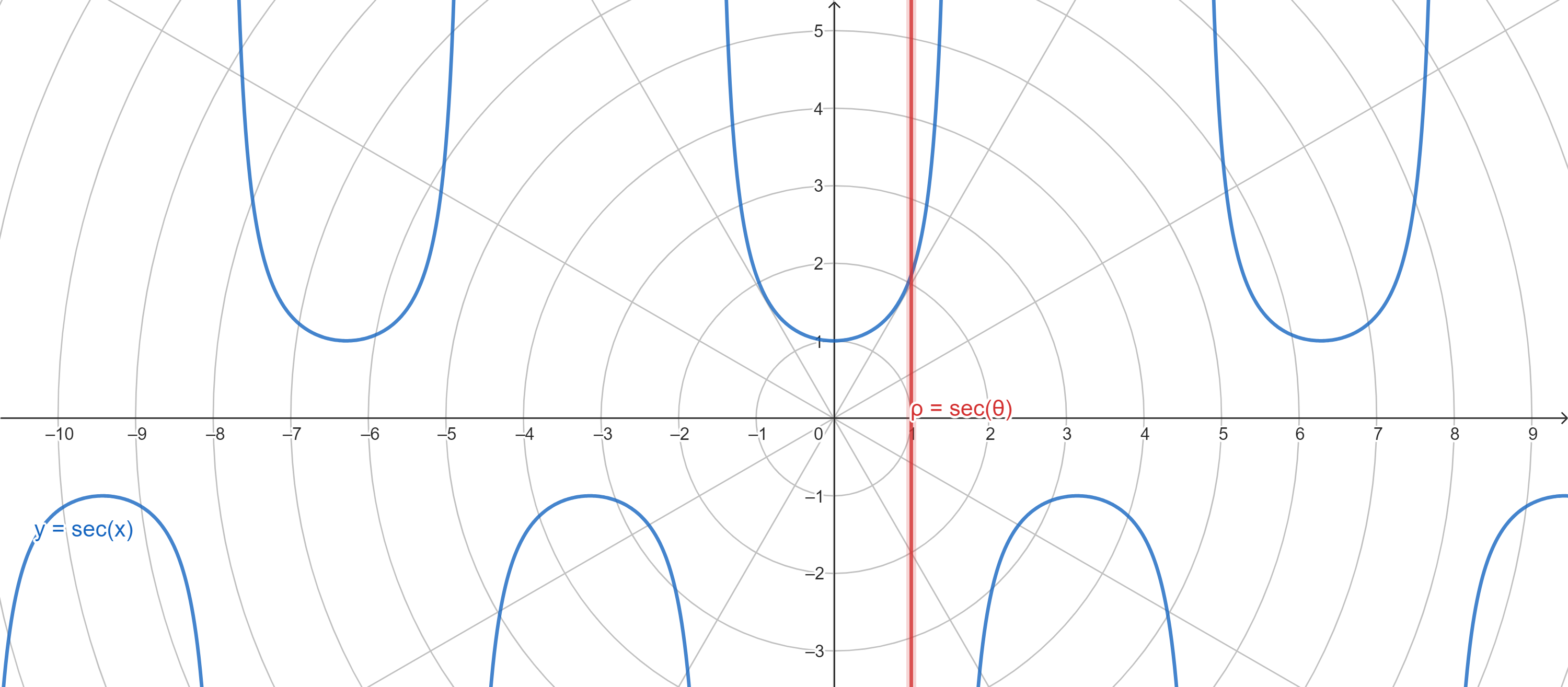
- 余割 csc
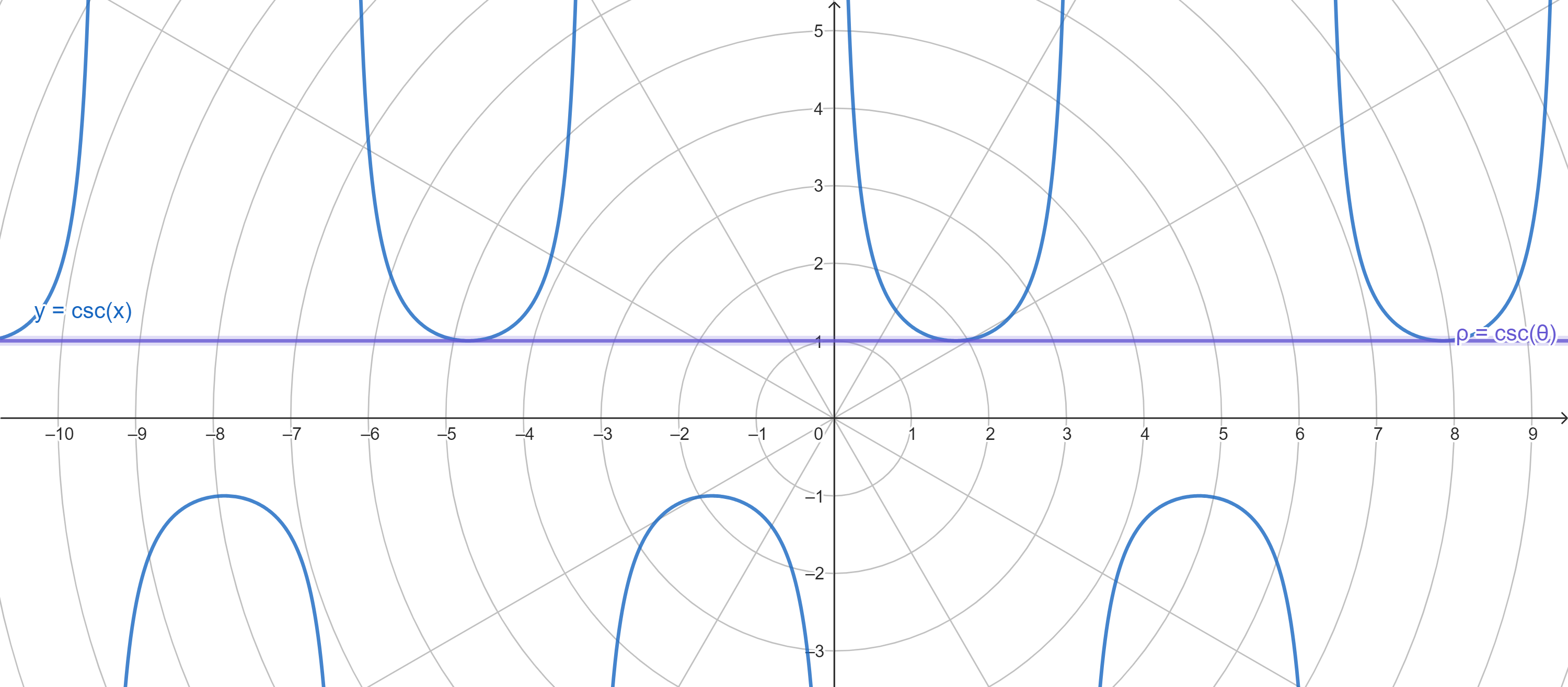
2. 常见的特殊角的三角函数值
| $0$ | $\frac{1}{6}\pi$ | $\frac{1}{4}\pi$ | $\frac{1}{3}\pi$ | $\frac{1}{2}\pi$ | $1\pi$ | $\frac{3}{2}\pi$ | |
|---|---|---|---|---|---|---|---|
| $\sin$ | $0$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ | $0$ | $-1$ |
| $\cos$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ | $-1$ | $0$ |
| $\tan$ | $0$ | $\frac{\sqrt{3}}{3}$ | $1$ | $\sqrt{3}$ | undefined | $0$ | undefined |
| $\cot$ | undefined | $\sqrt{3}$ | $1$ | $\frac{\sqrt{3}}{3}$ | $0$ | undefined | $0$ |
| $\sec$ | $1$ | $\frac{2\sqrt{3}}{3}$ | $\sqrt{2}$ | $2$ | undefined | $-1$ | undefined |
| $\csc$ | undefined | $2$ | $\sqrt{2}$ | $\frac{2\sqrt{3}}{3}$ | $1$ | undefined | $-1$ |
3. 诱导公式 Induction Formula
3.1 对称
| 反射于$\theta=0$(负角) | 反射于$\theta=\dfrac{\pi}{4}$(余角) | 反射于$\theta=\dfrac{\pi}{2}$(补角) | 反射于$\theta=\dfrac{3\pi}{4}$ |
|---|---|---|---|
| $\sin(0-\theta) = -\sin\theta$ | $\sin(\dfrac{\pi}{2}-\theta) = \cos\theta$ | $\sin(\pi-\theta) = \sin\theta$ | $\sin(\dfrac{3\pi}{2}-\theta) = -\cos\theta$ |
| $\cos(0-\theta) = \cos\theta$ | $\cos(\dfrac{\pi}{2}-\theta) = \sin\theta$ | $\cos(\pi-\theta) = -\cos\theta$ | $\cos(\dfrac{3\pi}{2}-\theta) = -\sin\theta$ |
| $\tan(0-\theta) = -\tan\theta$ | $\tan(\dfrac{\pi}{2}-\theta) = \cot\theta$ | $\tan(\pi-\theta) = -\tan\theta$ | $\tan(\dfrac{3\pi}{2}-\theta) = \cot\theta$ |
| $\cot(0-\theta) = -\cot\theta$ | $\cot(\dfrac{\pi}{2}-\theta) = \tan\theta$ | $\cot(\pi-\theta) = -\cot\theta$ | $\cot(\dfrac{3\pi}{2}-\theta) = \tan\theta$ |
| $\sec(0-\theta) = \sec\theta$ | $\sec(\dfrac{\pi}{2}-\theta) = \csc\theta$ | $\sec(\pi-\theta) = -\sec\theta$ | $\sec(\dfrac{3\pi}{2}-\theta) = -\csc\theta$ |
| $\csc(0-\theta) = -\csc\theta$ | $\csc(\dfrac{\pi}{2}-\theta) = \sec\theta$ | $\csc(\pi-\theta) = \csc\theta$ | $\csc(\dfrac{3\pi}{2}-\theta) = -\sec\theta$ |
注:$\sin \theta = \cos(\dfrac{\pi}{2} - \theta)$ 的证明在这里。
3.2 位移和周期
| 位移$\dfrac{\pi}{2}$(增加π/2相位) | 位移$\pi$(对角) | 位移$\dfrac{3\pi}{2}$ | 位移$2\pi$ (终边相同的角) |
|---|---|---|---|
| $\sin(\theta+\dfrac{\pi}{2}) = \cos\theta$ | $\sin(\theta+\pi) = -\sin\theta$ | $\sin(\theta + \dfrac{3\pi}{2}) = -\cos\theta$ | $\sin(\theta + 2\pi) = \sin\theta$ |
| $\cos(\theta+\dfrac{\pi}{2}) = -\sin\theta$ | $\cos(\theta+\pi) = -\cos\theta$ | $\cos(\theta + \dfrac{3\pi}{2}) = \sin\theta$ | $\cos(\theta + 2\pi) = \cos\theta$ |
| $\tan(\theta+\dfrac{\pi}{2}) = -\cot\theta$ | $\tan(\theta+\pi) = \tan\theta$ | $\tan(\theta + \dfrac{3\pi}{2}) = -\cot\theta$ | $\tan(\theta + 2\pi) = \tan\theta$ |
| $\cot(\theta+\dfrac{\pi}{2}) = -\tan\theta$ | $\cot(\theta+\pi) = \cot\theta$ | $\cot(\theta + \dfrac{3\pi}{2}) = -\tan\theta$ | $\cot(\theta + 2\pi) = \cot\theta$ |
| $\sec(\theta+\dfrac{\pi}{2}) = -\csc\theta$ | $\sec(\theta+\pi) = \sec\theta$ | $\sec(\theta + \dfrac{3\pi}{2}) = \csc\theta$ | $\sec(\theta + 2\pi) = \sec\theta$ |
| $\csc(\theta+\dfrac{\pi}{2}) = \sec\theta$ | $\csc(\theta+\pi) = \csc\theta$ | $\csc(\theta + \dfrac{3\pi}{2}) = -\set\theta$ | $\csc(\theta + 2\pi) = \csc\theta$ |
这些公式有一句著名的口诀:奇变偶不变,符号看象限。“奇变偶不变”指的是,如果括号内增加π/2的奇数倍,改变函数名(如$\sin$变成$\cos$),偶数倍则不变;而“符号看象限”指的是,只需要假设$\theta$是第一象限的角(这样θ的三角函数必定为正),而观察公式变换后$\theta + \dfrac{n\pi}{2}$在对应象限的三角函数的符号,例如$\sin(\theta + \pi)$,θ转动π rad后到达第三象限,而第三象限的正弦是负数,所以$\sin$前加负号,$sin(θ+π)=−sinθ$。Ref
4. 六边形
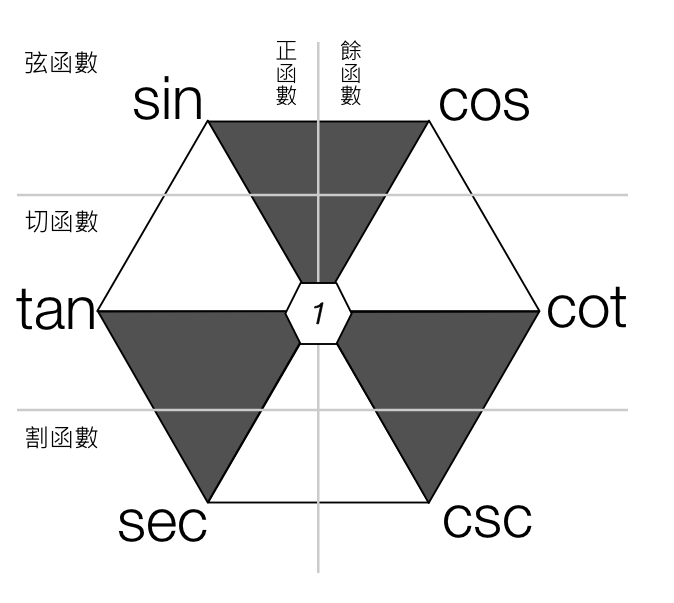
倒数关系
- $\sin\alpha \csc\alpha = 1$
- $\cos\alpha \sec\alpha = 1$
- $\tan\alpha \cot\alpha = 1$
平方和关系
- $\sin^2\alpha + \cos^2\alpha = 1$ (毕达哥拉斯三角恒等式)
- $\tan^2\alpha + 1 = \sec^2\alpha$
- $1 + \cot^2\alpha = \csc^2\alpha$
相邻三个值的关系(当前值等于往右第一个值除以往右第二个值,当前值等于相邻两个值的积)
- $\tan\alpha = \dfrac{\sin\alpha}{\cos\alpha} \iff \sin\alpha = \tan\alpha \cos\alpha$
- $\sin\alpha = \dfrac{\cos\alpha}{\cot\alpha} \iff \cos\alpha = \sin\alpha \cot\alpha$
- $\cos\alpha = \dfrac{\cot\alpha}{\csc\alpha} \iff \cot\alpha = \cos\alpha \csc\alpha$
- $\cot\alpha = \dfrac{\csc\alpha}{\sec\alpha} \iff \csc\alpha = \cot\alpha \sec\alpha$
- $\csc\alpha = \dfrac{\sec\alpha}{\tan\alpha} \iff \sec\alpha = \csc\alpha \tan\alpha$
- $\sec\alpha = \dfrac{\tan\alpha}{\sin\alpha} \iff \tan\alpha = \sec\alpha \sin\alpha$
5. 和差恒等式
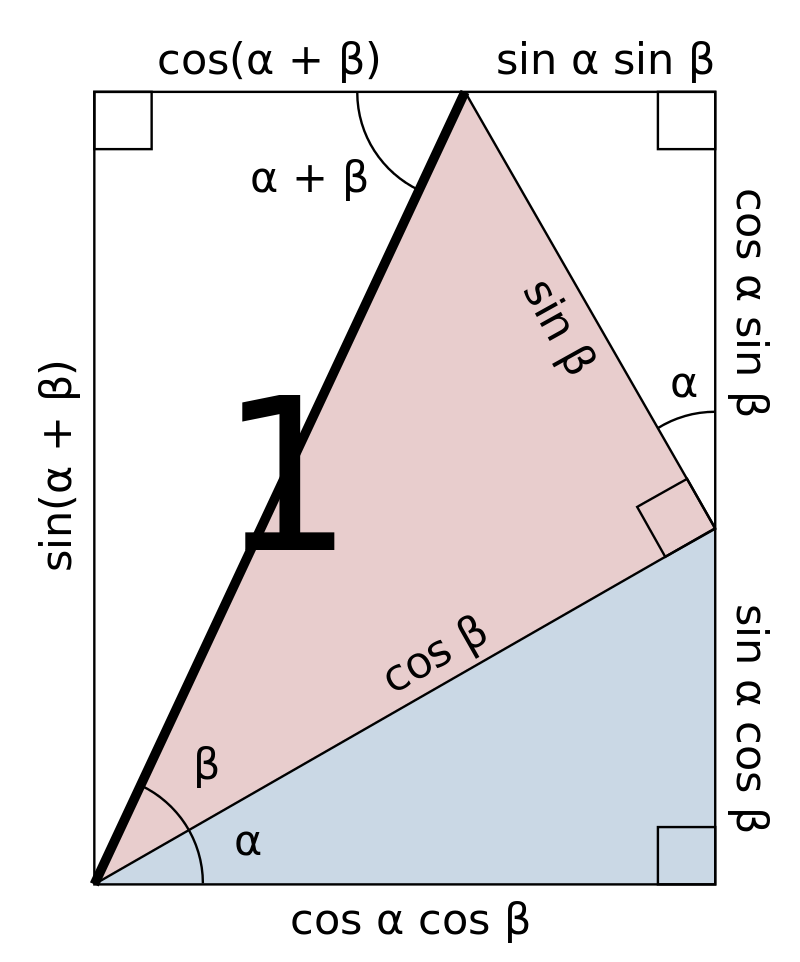
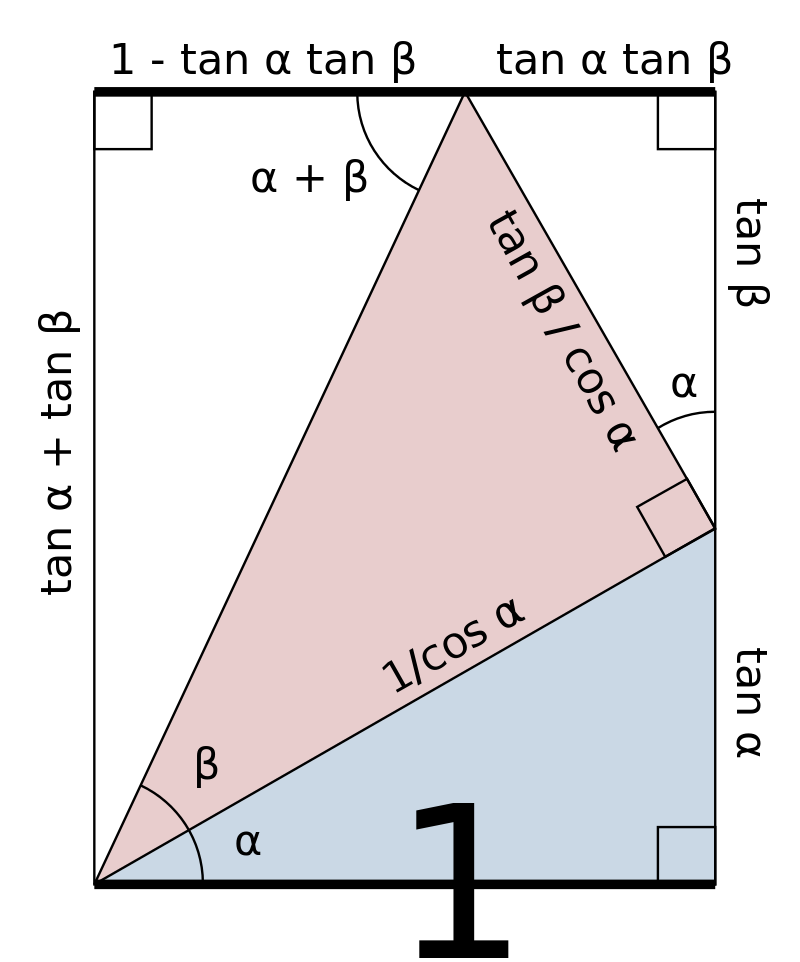
这里的两个图形证明虽然只展示了比较特殊的情况,但也非常不错,想当年我的老师可能因为这图并非完整证明而没有介绍给我们,不过也可能是他真的不晓得的,毕竟当年没有互联网,查点资料还是比较麻烦的。时间飞快,这一晚,就是二十多年。
- 正弦 $\sin(\alpha \pm \beta )=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta$
- 余弦 $\cos(\alpha \pm \beta )=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta$ (证明在此)
- 正切 $\tan(\alpha \pm \beta )={\dfrac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta}}$
- 余切 $\cot(\alpha \pm \beta )={\dfrac {\cot \alpha \cot \beta \mp 1}{\cot \beta \pm \cot \alpha }}$
- 正割 $\sec(\alpha \pm \beta )={\dfrac {\sec \alpha \sec \beta }{1\mp \tan \alpha \tan \beta }}$
- 余割 $\csc(\alpha \pm \beta )={\dfrac {\csc \alpha \csc \beta }{\cot \beta \pm \cot \alpha }}$
二倍角公式
- $\sin(2\alpha) = 2 \sin \alpha \cos \alpha$
- $\cos(2\alpha) = \cos^2 \alpha - \sin^2 \alpha = 2\cos^2 \alpha - 1 = 1 - 2\sin^2 \alpha$
- $\tan(2\alpha) = \dfrac{2\tan \alpha}{1 - \tan^2 \alpha}$
三倍角公式
- $\sin(3\alpha) = 3 \sin \alpha - 4 \sin^3 \alpha$
- $\cos(3\alpha) = 4 \cos^3 \alpha - 3 \cos \alpha$
半角公式(降幂公式)
- $\sin^2{\dfrac{\theta}{2}} = \dfrac{1 - \cos \theta}{2} \Rightarrow \sin{\dfrac{\theta}{2}} = \pm \sqrt{\dfrac{1 - \cos \theta}{2}}$
- $\cos^2{\dfrac{\theta}{2}} = \dfrac{1 + \cos \theta}{2} \Rightarrow \cos{\dfrac{\theta}{2}} = \pm \sqrt{\dfrac{1 + \cos \theta}{2}}$
- $\tan^2{\dfrac{\theta}{2}} = \dfrac{1 - \cos \theta}{1 + \cos \theta} \Rightarrow \tan{\dfrac{\theta}{2}} = \pm \sqrt{\dfrac{1 - \cos \theta}{1 + \cos \theta}}$
- $\tan{\dfrac{\theta}{2}} = \dfrac{\sin \theta}{1+\cos \theta} = \dfrac{1 - \cos \theta}{\sin \theta}$(注意定义域的变化)
6. 积化和差 product-to-sum
通常,我们提到的积化和差公式只涉及$\sin$和$\cos$相关的四个公式,它们都是从前面提到的和差恒等式推出的。
- $\sin \alpha \sin \beta = -\dfrac{\cos(\alpha + \beta) - \cos(\alpha - \beta)}{2}$
- $\sin \alpha \cos \beta = \dfrac{\sin(\alpha + \beta) + \sin(\alpha - \beta)}{2}$
- $\cos \alpha \sin \beta = \dfrac{\sin(\alpha + \beta) - \sin(\alpha - \beta)}{2}$
- $\cos \alpha \cos \beta = \dfrac{\cos(\alpha + \beta) + \cos(\alpha - \beta)}{2}$
7. 和差化积 sum-to-product
通常,这里也只是记录4个涉及$\sin$和$\cos$的公式,它们都可以通过上面积化和差的几个公式直接加减推出。
- $\sin \alpha + \sin \beta = 2\sin(\dfrac{\alpha + \beta}{2})\cos(\dfrac{\alpha - \beta}{2})$
- $\sin \alpha - \sin \beta = 2\cos(\dfrac{\alpha + \beta}{2})\sin(\dfrac{\alpha - \beta}{2})$
- $\cos \alpha + \cos \beta = 2\cos(\dfrac{\alpha + \beta}{2})\cos(\dfrac{\alpha - \beta}{2})$
- $\cos \alpha - \cos \beta = -2\sin(\dfrac{\alpha + \beta}{2})\sin(\dfrac{\alpha - \beta}{2})$
这几个公式,也可以通过把$\alpha$看成$\dfrac{\alpha + \beta}{2} + \dfrac{\alpha - \beta}{2}$,把$\beta$看成$\dfrac{\alpha + \beta}{2} - \dfrac{\alpha - \beta}{2}$,然后通过前面提到的和差恒等式直接相加得出。
8. 万能公式
用 $\tan{\dfrac{\alpha}{2}}$ 表示 $\sin \alpha$, $\cos \alpha$, $\tan \alpha$
- $\sin \alpha = \dfrac{2\tan{\dfrac{\alpha}{2}}}{1+\tan^2{\dfrac{\alpha}{2}}}$
- $\cos \alpha = \dfrac{1-\tan^2{\dfrac{\alpha}{2}}}{1+\tan^2{\dfrac{\alpha}{2}}}$
- $\tan \alpha = \dfrac{2\tan{\dfrac{\alpha}{2}}}{1-\tan^2{\dfrac{\alpha}{2}}}$
Ref:
- 维基百科·三角恒等式
- List of trigonometric identities (Wikipedia)
- 三角公式 (Easymath-wiki)