Cao Yi
面积最大的矩形
昨天(2023.07.15)和Charles讨论课本上介绍长度单位的文章,其中提到了英寸(inch)。我们想到电子产品的屏幕是按英寸来算的,但是屏幕的长宽比有4:3, 16:9等等不同的比例,那同样是23英寸的屏幕,长宽比不同,面积相同吗?
我们进一步讨论了这个问题,并把问题抽象为:如果一个矩形的对角线是一定的,那这个矩形在怎样的情形下面积最大?
根据矩形的面积公式,矩形的面积为长宽之积,所以,我们把问题进一步明确化:如果一个矩形的对角线是一定的,那这个矩形的长和宽比例为多少时,矩形面积最大?
这时我们已经画了一些图,隐隐约约感觉可能是长宽相等,即矩形为正方形时,面积最大,但我们此时还不能证明。
然后我们各自思考演算,找到了矩形面积最大的条件。
1. Charles的证明
如图所示,将原矩形ABCD向两个长宽两个方向延长一倍成一个更大的矩形AEFG. B, I, H, D是大矩形AEFG所在边的中点。
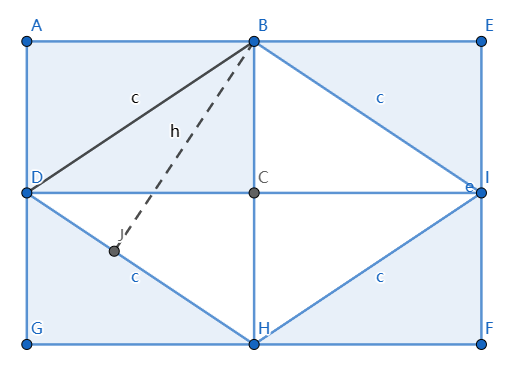
四个中点的连线在大矩形中构成了一个边长为c的菱形,同时也把大矩形分割成八个全等的三角形。
矩形ABCD的面积 $S_{ABCD}$ 为两个小三角形的面积之和。
菱形BIHD的面积 $S_{BIHD}$ 为四个小三角形面积之和。
所以 $S_{ABCD}=\dfrac{S_{BIHD}}{2}$
假设菱形BIHD的高BJ为h,则 $S_{BIHD}=ch$
h越接近c,$S_{BIHD}$ 越大。当h=c时,$S_{BIHD}$ 最大,此时菱形为正方形,此时 BC=CB,即矩形ABCD为正方形。
2. 我的证明
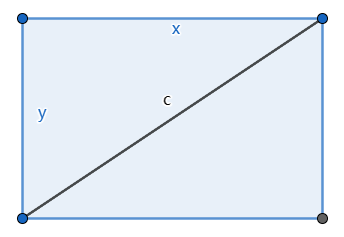
如图所示,不妨设矩形相邻两条边为x和y,对角线为定长c。
则 $x^2+y^2=c^2$
矩形的面积 $S=xy$
为了简化问题,不妨设 $c=1$
则 $x^2+y^2=1$
假设 $x=\sin{\theta}, y=\cos{\theta}$
则 $S=xy=\sin{\theta}\cos{\theta}=\dfrac{\sin{2\theta}}{2}$
显然 $\theta = \dfrac{\pi}{4}$时,$S_{max}=\dfrac{1}{2}$
此时
$x=\sin{\theta}=\sin{\dfrac{\pi}{4}}=\dfrac{\sqrt{2}}{2}$
$y=\cos{\theta}=\cos{\dfrac{\pi}{4}}=\dfrac{\sqrt{2}}{2}$
所以 $x=y$
即:矩形为正方形时,面积最大。
点评:以上推导过程虽然是正确的,但用到了三角函数的知识,需要中学的知识,Charles还无法完全理解。
不用三角函数
如果不用三角函数,则 $S=xy=x\sqrt{1-x^2}$
问题就转化为求曲线$x\sqrt{1-x^2}$的极值,这个其实还比较困难,但可以通过用GeoG作图大概感受下:
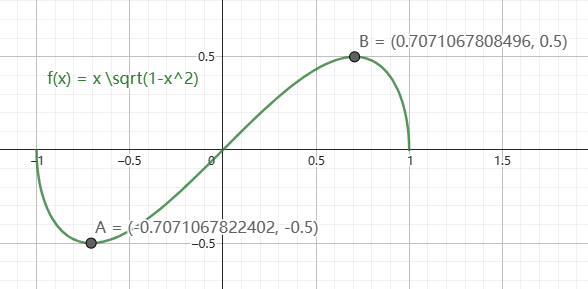
后记:一开始,Charles还误以为虽然长宽比不一样,但长宽的和是一样,他还误打误撞提了一个猜想——两数之积不大于两数之和一半的平方,经过我的证明,是正确的。