Cao Yi
正弦定理 Law of Sines
设$\triangle ABC$的三个角$\angle A$, $\angle B$和$\angle C$对应的三条边是a, b和c, R是三角形的外接圆的半径,则
$\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R$
证明
如下图,直线AO过圆心O交圆周于D,
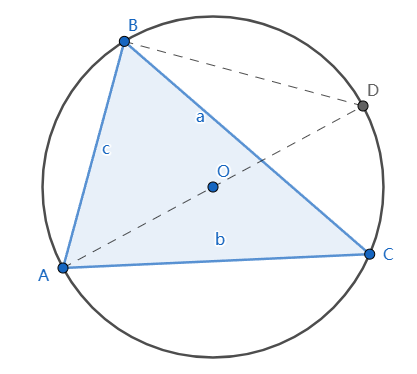
根据圆周角的性质,
$\angle ACB = \angle ADB$, $\angle ABD = \dfrac{\pi}{2}$
$\therefore \vert AB \vert = \vert AD \vert \sin{\angle ADB}=\vert AD \vert \sin{\angle ACB}=2R\sin{\angle ACB}$
即 $c=2R\sin{C}$
$\therefore \dfrac{c}{\sin C} = 2R$
同理可证
$\therefore \dfrac{a}{\sin A} = 2R$
$\therefore \dfrac{b}{\sin B} = 2R$
$\therefore \dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R$
参考