Cao Yi
按月等额还款下的实际年利率计算方法
2025.02.14
昨天同事 Pony 说不同的 AI 工具计算年利率的结果不一样。他的问题是:
借款42000元,每个月需还款1813.57元,一共24个月还完,请问实际年化利率是多少?
AI 的错误回答
这个问题看起来非常简单,但AI的计算功能确实让人费解,我去验证了下:
这个差异让我有点吃惊,这两个 AI 都是平常我用得比较多的,感觉还不错的,不过,它们对同样问题,计算出来的差异居然这么大。
我的错误尝试
这个问题看起来确实简单,复利公式一套就解出来了。
复利公式:
假设每个周期利率是 $r$, 所借的本金是 $a$, 则第 $n$ 个周期结束,需要偿还的债务是 $a(1+r)^n$
带入到这里
- 本金是 $42000$
- 年利率假定是 $x$
- 还款周期数 $2$
- 最终还款额 $1813.57 \times 24 = 42000(1+x)^2$
这个方程很好解,算出来的结果(正数解)是 $\sqrt{\dfrac{1813.57 \times 24}{42000} -1} \approx 0.0180 = 1.8\%$. 这个值和前面AI的结果差很多。这个值是对的吗?
同事的解释
我把答案提供给同事后,他说我的计算肯定是错的。他举了一个例子:
张三借给李四10000元,月底年利息是20%,张三的还款时间会影响到实际利率。
- 如果李四一年后直接还张三12000,那年利率就是20%
- 如果李四半年后就还张三12000,那实际的年利率其实是40%
- ……
这个解释让我陷入深思,当然我也晓得前面错了。我没有意识到实际还款周期是按月的,我的计算却是按年的,这和复利公式的使用条件不符。我打算下班之后再算一下。
回家后的计算——通解
我准备先把这个问题一般化,求一个通解。问题泛化为:
已知:借款a元,每月还m元,还n月,还完。
求: 实际的年利率。
因为实际还款是按月的,所以可以使用复利公式先算月利率,再算年利率。
假设月利率为$r$, 第$i$月偿还的本金是$b_i$, 则每月偿还的总额为$m=b_{i}(1+r)^i$
解得 $b_{i} = \dfrac{m}{(1+r)^i}$
又,全部本金$a$为每月偿还的本金之和:$a=b_{1}+b_{2}+…+b_{n}$
即 $a=\dfrac{m}{1+r} + \dfrac{m}{(1+r)^2} + … + \dfrac{m}{(1+r)^n}$
即 $a=m\left[\dfrac{1}{1+r} + \dfrac{1}{(1+r)^2} + … + \dfrac{1}{(1+r)^n}\right]$
使用等比数列求和公式得 $a=m\cdot\dfrac{1 - \dfrac{1}{(1+r)^{n+1}}}{1-\dfrac{1}{1+r}}$
即 $a=m\cdot\dfrac{(1+r)^{n+1} -1}{(1+r)^{n+1} -(1+r)^{n}}$
在上面的方程中,本金$a$, 每月还款额$m$, 还款期数$n$ 都是已知的,所以可以解出月利率$r$.
假设年利率为$R$, 则根据复利公式得 $(1+r)^{12} = 1 + R$
所以年利率为 $R = (1+r)^{12} - 1$
最初的问题
回到最初的问题
借款42000元,每个月需还款1813.57元,一共24个月还完,请问实际年化利率是多少?
这里
- $a=42000$
- $m=1813.57$
- $n=24$
代入公式 $a=m\cdot\dfrac{(1+r)^{n+1} -1}{(1+r)^{n+1} -(1+r)^{n}}$ 得:
$42000=1813.57\left[\dfrac{(1+r)^{25} -1}{(1+r)^{25} -(1+r)^{24}}\right]$
使用 Mathway 解出 $r \approx 0.0064868$
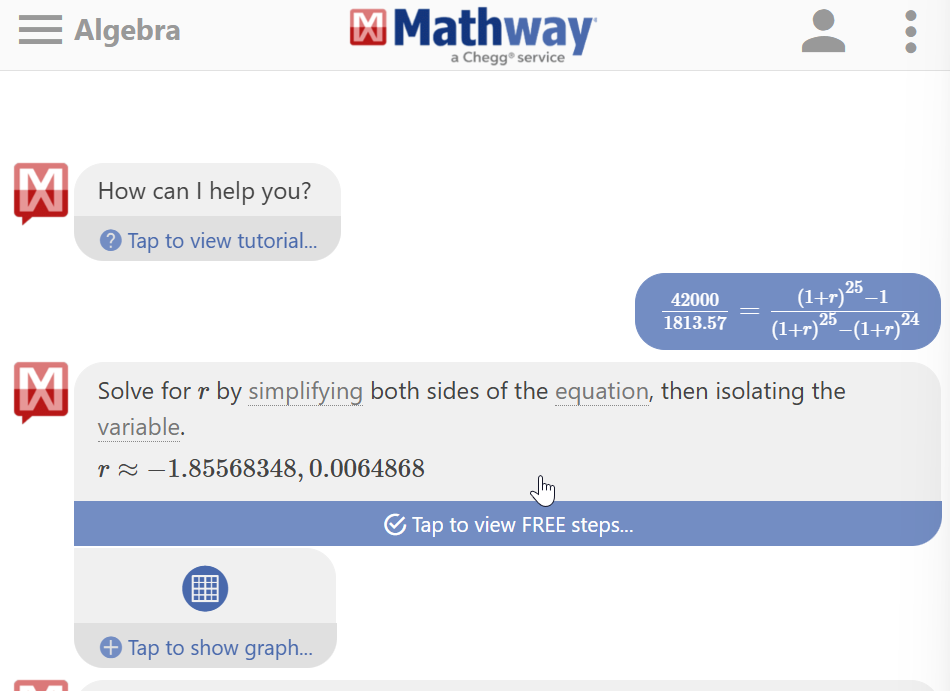
所以年利率 $R = (1+r)^{12} - 1 \approx {1.0064868}^{12} - 1 \approx 0.08067972 \approx 8.07\%$
这个值和之前简单计算的年利率1.8%差了很多。
这个问题也提醒个人注意,在向银行贷款时,要明确自己的还款周期,了解个人需要承担的真实利息成本。
计算工具
本文用到了以下网络计算工具:
- 微软 Math Solver: https://mathsolver.microsoft.com/en
- Mathway: https://www.mathway.com/Algebra