Cao Yi
大边对大角,大角对大边
三角形的边的大小顺序和角的大小顺序是一致的。
在$\triangle ABC$中,如果 $a \geq b \geq c$ 则 $\angle A \geq \angle B \geq \angle C$,反之亦然。
这个命题很直观,很简单,很实用,它可以用正弦定理证明。
证明
1. 大角对大边
不妨通过比较$\angle A$和$\angle B$来说明,假设$\angle A \leq \angle B$
【第一种情形】
当$\angle A$和$\angle B$都是锐角
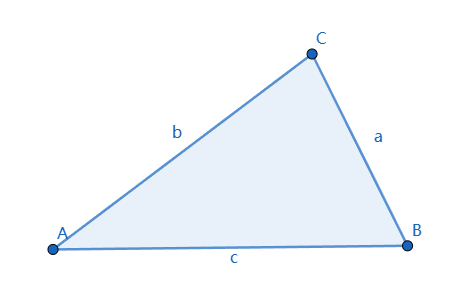
根据正弦定理
$\dfrac{a}{\sin A}=\dfrac{b}{sin B}$
$\therefore \dfrac{a}{b} = \dfrac{\sin A}{\sin B}$
又 $\because \sin x$在$[0, \dfrac{\pi}{2}]$是单调递增的
$\therefore a \leq b$
【第二种情形】
当$\angle A$是锐角,$\angle B$是直角。
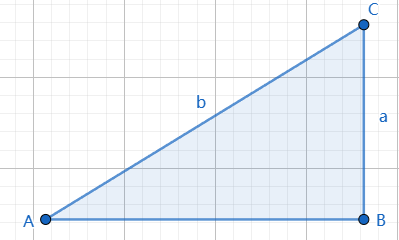
直角边小于斜边,所以$a \lt b$
【第三种情形】
当$\angle A$是锐角,$\angle B$是钝角。
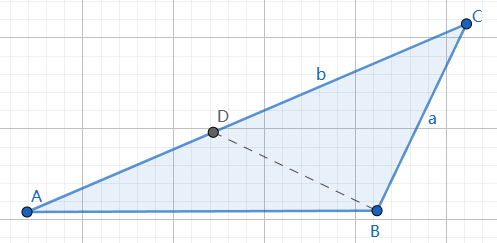
过B点作BC的垂线DB
$\vert BC \vert \lt \vert DC \vert \lt \vert AC \vert$
即得 $a \lt b$
综上三种情况,大角对大边得证。
2. 大边对大角
不妨通过比较a和b来说明,当$a=b$时,$\angle A = \angle B$. (参三角形等边对等角)
下面讨论$a \neq b$的情形,假设$a \lt b$
无论是锐角直角还是钝角三角形,都可以用下面的证明。
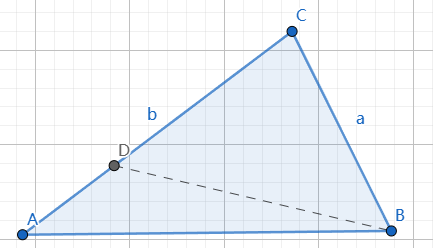
在长边CA上作线段CD,使$\vert CD \vert = \vert CB \vert = a$
$\therefore \angle ABC \gt \angle DBC = \angle BDC \gt \angle A$
即得 $\angle A \lt \angle B$