Cao Yi
证明 $\cos(\alpha - \beta)=\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)$
2026.01.09
这个公式最早是高中学到的,然后未经严格证明就懵懵懂懂在用了,现在我来把证明补上。如果把人生比作爬山,我已经在走下山的路了,等我死的时候,连这么简单的问题都没真的搞懂过,就太遗憾了。
-【已知】:$\alpha, \beta \in \mathbb{R}$ -【求证】:$\cos(\alpha - \beta)=\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)$
证明
单位圆上,任意角度 $\theta$ 对应的点坐标是 $(\cos(\theta), \sin(\theta))$.
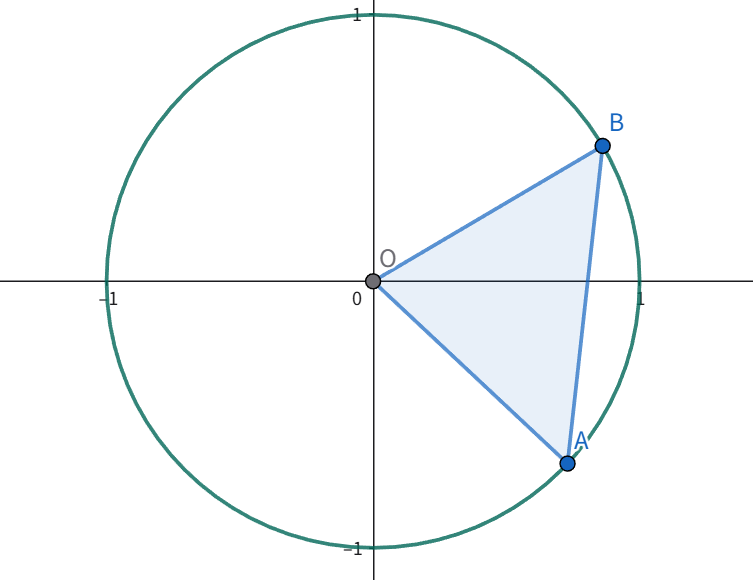
现在我们在单位圆上任取两点:
- 点 $A$ 对应的角度为 $\alpha$,坐标为 $(\cos(\alpha), \sin(\alpha))$
- 点 $B$ 对应的角度为 $\beta$,坐标为 $(\cos(\beta), \sin(\beta))$
根据平面坐标系中的两点的距离公式,可知:
$\vert AB\vert ^2 = (cos(\alpha) - \cos(\beta))^2 + (\sin(\alpha) - \sin(\beta))^2$
展开并利用公式 $\sin^2(\theta) + \cos^2(\theta) = 1$ 得:
$\vert AB\vert ^2 = 2 - 2(\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta))$
又根据余弦定理,在 $\triangle{OAB}$ 中($\vert OA\vert =\vert OB\vert =1$,$\overrightarrow{OA}$ 和 $\overrightarrow{OB}$ 的夹角为 $\vert \alpha - \beta\vert $):
$\vert AB\vert ^2 = \vert OA\vert ^2 + \vert OB\vert ^2-2\vert OA\vert \vert OB\vert \cos(\alpha-\beta)=2-2\cos(\alpha-\beta)$
综上可得:$\cos(\alpha - \beta)=\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)$
证毕。
扩展说明
根据 $\cos(\alpha - \beta)=\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)$
以 $-\beta$ 代 $\beta$,可得 $\cos(\alpha + \beta)=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)$
以 $\dfrac{\pi}{2} - \alpha$ 代 $\alpha$,可得:
$\cos(\dfrac{\pi}{2} - \alpha - \beta)=\cos(\dfrac{\pi}{2} - \alpha)\cos(\beta)+\sin(\dfrac{\pi}{2} - \alpha)\sin(\beta)$
- 左边:$\cos(\dfrac{\pi}{2} - \alpha - \beta)=\cos(\dfrac{\pi}{2} - (\alpha + \beta)) = \sin(\alpha + \beta)$
- 右边可以化作:$\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)$
即得到正弦的和角公式:$\sin(\alpha + \beta)=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)$
再以 $-\beta$ 代 $\beta$ 代入上式,可得:$\sin(\alpha - \beta)=\sin(\alpha)\cos(\beta)-\cos(\alpha)\sin(\beta)$
这里我们只证明了一个公式就得到了另外三个,实际上这四个公式可以认为是等价的,只要其中一个成立,另外三个都成立。下面再整齐地列出这四个公式:
- $\cos(\alpha - \beta)=\cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta)$
- $\cos(\alpha + \beta)=\cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta)$
- $\sin(\alpha + \beta)=\sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta)$
- $\sin(\alpha - \beta)=\sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta)$
还可以继续扩展成其他三角公式,可以参本站记录的三角函数公式 Trigonometric Formulas。